this page in english diese Seite auf deutsch

Sense and nonsense of night set-back

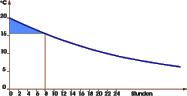cooling down Night time heating reduction is a night set back of heating power by a time controlled programmable thermostat.

The room temperature has evident effect on heating costs but night setback won't give appreciable savings.

 

Influence of room temperature

For every degree celsius increased room temperature throughout whole day you have to expect additional 5% heating cost.

It's easy to recalculate.

The temperature difference between inside and outside is proportional to heat emission. This dissipation causes heating costs.

Room temperature is assumed to 20°C. It's a nice even number. And outside?

The medium temperature in winter is 0°C. (Temperatures lower then -15°C are truely possible in Central Europe, but rarely. Children are looking forward to snow - long times because ist's seldom. About zero degree celsius is a usable assumption. In winter 2000/2001 here it has snowed one time - at easter!):

1961 to 1990 °C sunshine
hours		 mm rainfall
Jan 0.2 37 46
Feb 0.7 64 30
Mar 3.1 109 40
Apr 6.3 174 42
May 11.3 245 46
Jun 15.0 247 59
Jul 16.8 234 71
Aug 16.7 225 59
Sep 13.9 157 54
Oct 9.9 105 42
Nov 5.3 53 52
Dec 1.9 37 48

Weather in Warnemünde
(Source: Deutscher Wetterdienst, showcase)

Calculation example 1: whole day only 20 instead of 21°C room temperature
While keeping 21°C inside living rooms and having outside 0°C there is a temperature difference of 21 degree to overcome.

But if keeping 20°C inside living rooms then the temperature difference is only 20 degrees. 


	21 degr
	------- = 1.05 = 105% = 100% + 5%
	20 degr
The heat dissipation at 21°C would be 5% higher then at 20°C.

To relingquish only one degree room temperature enables 5% energy saving and therefore cost saving.  

Temperature und heat

Temperature is strongly to distict from heat. Heat is a form of energy. Temperature is a property of a physical object. While warming up such object (with mass m) it's feeded thermal energy (symbol Q) . An object with high temperature collects and saves this energy, and delivers it while cooling down. This capability of accumulating thermal energy is named effective heat capacity. The specific heat capacity is a material property (symbol c).

The connection between changes in temperature (symbol /\T) and thermal energy is given by the base equation of thermodynamics: 

	Q = m · c · /\T
 
(Sorry, I have to circumscribe the greek letter DELTA as /\ for an acceptable representation in all browsers)

As long as the feeded thermal energy ist right equal to the disappeared energy as long the temperature stays constant.
While the energy balance is unbalanced then the temperature is changing. If after a time a compensation is achieved and the starting temperature is reached again then the energy balance - averagely - was balanced.
Storing heat
The storing of thermal energy is known for example from hot-water bottle. First the water is feeded heat by fire below the kettle, increasing it's temperature. Afterwards the water is delivering the heat while decreasing it's temperature.
Storing coldness
The same is possible with coldness (negative heat). We store coldness for picnic in cold packs. First their heat ist detracted inside a refrigerator. They cool down. While they are absorbing heat from their environment (keeping cola und chocolate fresh) they warm up again.
Keeping temperature constant
To keep a warm object warmer than it's environment it's covered with a heat insulating coat. That's the same thing at a thermosbottle, a sleeping bag or a home. At a home the walls prevent cooling - mostly very good but not completely.

The heat surrendered at the surface of a home has to be replaced by heating to keep the room temperature stable. The result is a balance: While the room temperature doesn't changes we can be sure the heating supplies exact as much heat as is surrendered. Otherwise the temperature would raise or fall depending on supplied versus surrendered thermal energy, i.e. if there is more heating power then loss thru walls, windows, ventilation or waste water or if there is less heating power.

The supply of thermal energy has stringently to be exact equal the surrendered energy otherwise the original temperature never could be reached again. In other words: As much thermal energy as at night surrendered thru the walls has to be supplied by heating to reach next day the same room temperature like previous day.

To determine the cost-saving by night set-back we only have to calculate the heat dissipation because the heat supply is exact equal.

"keeping off the heating is saving energy" - that's the mistake, a fallacy.

Even while the heating pauses at night - the surrendering of thermal energy is continued. The heat transfer ist proportional to the difference of temperatures. As long as inside it's still warmer than outside as long thermal energy is surrendered. As bigger as the temperature gradient is it happens faster.

 

Night set-back

For sleeping smaller room temperatures are pleasantly felt and recommended than during the day. And if it's a little bit cooler in all rooms at night nobody is discommoded. Thus the heating is reduced in the evening, the button at the heating element is turned back. The room temperature lowers itself - it's almost not noticeable -. In the morning the heating element is turned on again. This purposely lowering of the room temperature during night is known as night set-back.

This idea suggests itself. if heating ist turned off at night then it doesn't consume fuel all night.

But, is it actually possible to save a third of fuel, if during 8 of 24 hours heating is off? In a tent, a wooden site trailer, a green house or an old barrack that actually nearly applies, because there the temperature sinks almost down to outside temperature, At night there it's inside just as cold as outside. And where no temperature gradient can be found, there is no loss of thermal energy.

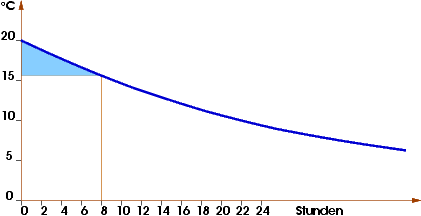diagram: falling temperature But inside a well isolated house the warmth is kept excellently. If the heating is broken during two frosty days, the room temperature falls down to 12°C or perhaps 8 or 6°C. In any case temperature will sink during 8 hours only around a few degree. It's worth it to recalculate.

If the room temperature is lowered on 16°C at night, the heating suspends, until the temperature sank down from 20°C to 16 °C. That can last for a long time, if solid inner walls and heavy furnishings stored the warmth from the day like a tiled stove an now slowly deliver (in physics it's named a high termal capacity).

Calculation example 2: outside 0°C, heating off at night
Outside there are 0°C again. While heating is off room temperature sinks within the 8 hours of night-time heating reduction continuosly from 20° to 16°C (it's 20%).

At the beginnig of the night as long as still 20°C happen it's still warm inside. There is no saving, 0%

At the end of the night-time heating reduction the temperature difference amounts to only 16°C. The heat emission is decreased from 100% to 


	16
	-- = 0.8 = 80% = 100% - 20%
	20
Apparently 20% saving!

But this is correct only in the morning, at the end of the night-time heating reduction, after the room temperature really already sank to 16°C. As average value over the whole night results a saving of 10%. 


	evenig+morning	 0% + 20%
	-------------- = -------- = 10%
	      2		     2

However only eight out of 24 hours are night. Saving only by night-time heating reduction thus becomes 


	       8h
	10% · --- = 3.3%
	      24h
not exceeded.

Altogether this example results in merely 3.3% energy saving round 24 hours.

Calculation example 3: outside frosty -10°C, heating off at night
Once it's really cold, physical laws are unchanged..

In this example we (with otherwise same conditions as in example 2) calculate whith an outside temperature of -10°C (thus 30°C temperature difference). Also in this very cold night the heating pauses. Then the room temperature sinks over night just like in example 2 around 20%. But that is no longer only 4°. It's a third more. 


	20% · 30°C = 6°C
During 8 hours of night set-back the room temperature is falling continuosly from +20°C to 16°C. The temperature difference decreases from 30°C to only 22°C, As in example 1 the heat emission has lowered to: 

	24
	-- = 0.8 = 80% = 100% - 20%
	30
Averaged over the whole night again results in a saving of 10% through the night. And a third over 24 hours.

Also in this example only 3,3% energy conservation remain over 24 hours. And that only if at the end of the night +14°C is tolerated as room temperature!

Calculation example 4: outside frosty -10°C, limited night-time heating reduction
But it should not cool down too much inside home during night. That's why we let the heating nevertheless still work a little around a cold night with an outside temperature of -10°C Thereby saving is naturally anymore smaller.

The room temperature from during the day 20°C may sink during the night-time heating reduction at the most down to 16°C (the 14°C as in example 3 is too cold). After 8 hours without heating the temperature (as in example 3) would be around 20% that is 6°C fallen. The granted 4°C is already reached after 5.3 hours. 


	 6°      4°
	--- =  -----
	8 h    5.3 h
At the end of these 5.3 hours the heat emission is sunken to 

	26
	-- = 0.867 = 86.7% = 100% - 13.3%
	30
on the average only half of it, thus during 5.3 hours 6.7% saving. From that time the heating maintains 16°C room temperature by supply of thermal energy. The continuous temperature difference of 26°C causes during 8 - 5.3 = 2.7 hours a heat emission from again 

	26
	-- = 0.867 = 86.7 % = 100% - 13.3%
	30
By way of calculation saving during the whole night results as the weighted means to 

	5.3 · 6.7% + 2.7 · 13.3%
	------------------------ = 8.9%
	      5.3 + 2.7
And during 24 hours on the average again only one third of it, only 3%.

On cold days possible saving by night-time heating reduction is proportionally much smaller than on less cold days Although on cold days a saving would be extra desirable and effective. By night-time heating reduction of acceptable 4°C it's arithmetically possible to reach heating cost savings from at the most 3% to 3.3%.  

Practical proof

Do you know someone, who can compute his heat requirement from well-known outside temperature exactly on 3%? Is there anybody, who can experimentally prove 3% fuel savings absolutely certain? The saving by night-time heating reduction is apriori only purely arithmetical, and is destroyed by contrary effects.  

Heating-up phase

If the nightly cool down caused by night set-back - as tiny as it may be - has to be compensated by heating in the morning within one or two hours, then a significant higher water temperature is to be driven, than would be necessary without night-time heating reduction. Depending upon boiler and heating elements that causes a lower efficiency. Higher water temperature implies evenly higher exhaust gas temperature and more losses.

How rapidly the 3% night time saving is wasted!

 

Wet walls

While cooling down outer walls during nighttime heating reduction, the dew temperature may be reached. Wetness sets down on the walls. That causes mould and increasing heating loss, the walls cool down further, that results in more wetness, the loss increases and so on.

That doesn't happen at the same time on the entire surface. In places, which are perhaps purely coincidentally somewhat more coldly, the self accelerating effect begins first and leads to spotting.  

Recommendation

It's understood to turn off the heating elements while window is open or tilted.
Perhaps the function "night set back" in heating systems nevertheless may be usual to give some rest to circulation pumps and all the equipment. This way energy isn't saved but lifetime of heating can be increased.
If the sun is forceful shining on an beautiful sunny day in the end of february or begin of march then the heating may be reduced a little on those days. Therefore the "night" set-back has to be set to forenoon i.e. 8 o'clock 'til 11 o'clock.
Because the heating had worked continuously during night, in the morning at eight o'clock it's comfortable warm. If the sun is shining then heating in't necessary, if the sun is not shining, heating restarts after three hours. Until then for sure it's warm inside.

 

Links:
see german original text
The given hotlinks refer to cited texts with intellectual property to their owners. The further content of referenced texts may differ from base idea of this page and may be object of disput (as this side also).
 

Contents

November 2010, A. Hok.
www.ahok.de/en/night-set-back.html
[valid HTML3.2 and CSS]