Gray code

The Gray code is a single-step code (i.e. a unit-distance code). It's often used in analog/digital conversion devices. Adjacent code patterns of Gray code differ in just only one bit to avoid ambiguity, i.e. consecutive code elements have a hamming distance of one.

Errors while read off, for example by oblique scanners, slightly different threasure values inside the detectors, delay and race conditions in logical circuits only give minimal effects while using Gray code.

In 1878 French man Émile Baudot (1845-1903) first presented this "cyclic permuted" code. It's named after Frank Gray ["Pulse Code Communication", U.S. Patent no. 2,632,058, March 17, 1953 (origin: uspto.gov) ].

Variations of the Gray code pursue special properties:

BCD codes (binary coded decimal):
Codes for a decimal digit, consisting of 10 code words (instead of 16 for Gray code), but still having only one transition from one measuring step to the next.

Code words 0 to 8 of the Glixon code are identical as in Gray code.
excess-3 gray code is a gray code displaced by 3 code steps, i.e. the first three and the last three code patterns have been dropped.
[don't confuse with excess-3 BCD code, also known as "stibitz code", named after George Robert Stibitz]
The second O'Brien code, the second Tompkins code and the Petherick code use neither code patterns "0000" nor "1111". That has practical advantages.
Three of the four bits of Tompkins's code may be scanned out of the same code stripe by three displaced detectors.

Excess Gray code, O'Brien code and Petherick code have mirrored three least significant bits. It's known as "reflected code". Inverting the MSB (most significant bit) gives the 9th-complement. That simplifies subtractions.

position (code word)	Gray code	decimal tetradic codes
position (code word)	Gray code	Glixon code	O'Brien code		Excess Gray code	Tompkins code		Petherick code
0	0000	0000	0000	0001	0010	0000	0010	0101
1	0001	0001	0001	0011	0110	0001	0011	0001
2	0011	0011	0011	0010	0111	0011	0111	0011
3	0010	0010	0010	0110	0101	0010	0101	0010
4	0110	0110	0110	0100	0100	0110	0100	0110
5	0111	0111	1110	1100	1100	1110	1100	1110
6	0101	0101	1010	1110	1101	1111	1101	1010
7	0100	0100	1011	1010	1111	1101	1001	1011
8	1100	1100	1001	1011	1110	1100	1011	1001
9	1101	1000	1000	1001	1010	1000	1010	1101
10	1111
11	1110
12	1010
13	1011
14	1001
15	1000

The regular gray code in n bits consists of 2ⁿ code words. To get a gray code with double length out of an existing gray code, the existing gray code is repeated in reverse order. Both halves create a loop (therefore the name "reflected code" or "cyclic permuted code"). The additional bit is the most significant bit (MSB), discrimining between both halves.

        two+two=four                    four+four=eight
 
           3    2                     7     6     5     4
        -----<-----                <-----<-----<-----<------
        | 10   11 |                | 100   101   111   110 |
        v    +    ^                v     +-----+-----+     ^
        | 00   01 |                | 000   001   011   010 |
        ----->-----                >----->----->----->----->
           0    1                     0     1     2     3

           15     14     13     12     11     10      9      8
        <------<------<------<------<------<------<------<------<
        | 1000   1001   1011   1010   1110   1111   1101   1100 |
        v      +------+------+------+------+------+------+      ^
        | 0000   0001   0011   0010   0110   0111   0101   0100 |
        >------>------>------>------>------>------>------>------>
            0      1      2      3      4      5      6      7

                           eight+eight=sixteen

The horizontal and the vertical neighbouring code patterns have a hamming distance of one. To create a shorter unit-distance code string, extremely left or right outside lying positions aren't used (gray excess code).

The 10 steps excess-3 code is constructed by ignoring the six left positions 0...2 and 13...15 of the 16 step Gray code and directly crossing over between position 12 and 3 as shown:

          (15)   (14)   (13)    12     11     10      9      8
                             <------<------<------<------<------<
          1000   1001   1011 | 1010   1110   1111   1101   1100 |
                             v      +------+------+------+      ^
          0000   0001   0011 | 0010   0110   0111   0101   0100 |
                             >------>------>------>------>------>
           (0)    (1)    (2)     3      4      5      6      7
 
                                       Excess-3 code

For example look at unit distance codes, having 360 or 720 elements to encode rotations:

360° require 9 bits. As zero-degree-position the gray code for 76 is used and for 359° the gray code for 435. (Gray code 9 bit cut at both sides by 76 steps equals 360 steps)
```
	(2^9 - 360)  /  2          =  76	Gray:    1101010
	2^9 - 76 - 1  =  76 + 359  = 435	Gray:  101101010	
```

720 steps (0.2°) require 10 bits. Zero is coded as 152 and 259.9° as 871.

	(2^10 - 720) / 2           = 152	Gray:   11010100
	2^10 - 152 - 1 = 152 + 719 = 871	Gray: 1011010100

Both times the resulting code is a unit-distance code, because there is only one bit changing even between first and last used code patterns.

The below given code for a "Mechanical encoder for digital measuring of length and angles" needs only a half number of code tracks than other codes, for example, 16 code words out of 2 instead of four tracks.

Herein an enhanced Gray code is described, where two bits are read out of each code track. That allows to reduce the numbers of code tracks to a half. This code can replace the well known Gray code resulting in smaller and cheaper sensor devices.

Title

Mechanical encoder for digital measuring of length and angles

"4" binary scanner for stripe 3 v v

"3" most significant stripe

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 2 3 4

"1" stripe of code
"2" binary scanner for stripe 1 ^ ^

Figure 1

Abstract

Every stripe of code is scanned on the encoder plate at two points with a special displacement. Therefore only half of the stripes of code are necessary.

A special code is used, that changes only one bit from one entry to the next when scanned on the displaced points. The most significant stripe of code is as the Gray code. On the other stripes of code the bit stream "1001110001100011" is used once or repeating. Scanning that bit stream displaced by 4 steps gives the bit stream "1100011000111001".

The encoder is smaller and cheaper than an Gray code encoder and can replace it.

Example

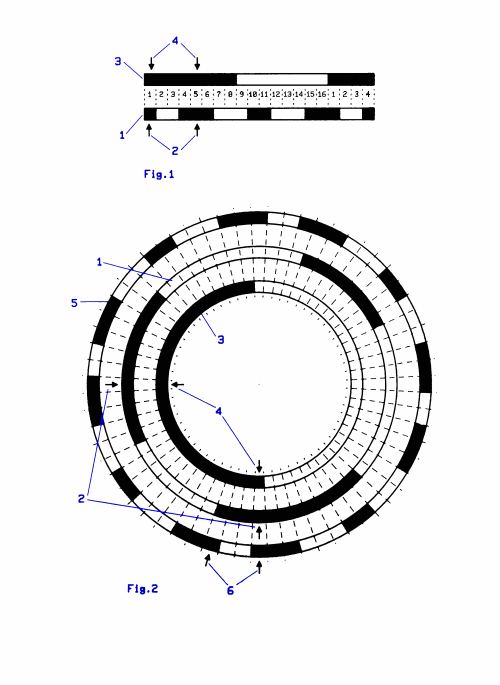
Figure 1 shows a code plate whith 16 steps. Figure 2 shows a circular code plate for measuring of angels whith 64 steps. The scanning points and their displacement are marked.

The most significant stripe of code "3" is as the well known Gray code. i.e. one half of the stripe is filled whith ones and the other half whith zeroes. For sixteen digital steps it's the bit stream "1111111100000000". This stripe of code ist scanned like the well known incremental code by two binary scanners having a fixed mechanical displacement of a quarter of the whole way.

The next stripe of code "1" (and all following stripes of code "5") carries the bit stream "1001110001100011". Also this stripe of code ist scanned by two binary scanners having a fixed mechanical displacement of a quarter of the whole way. Displaced scanning gives the bit stream "1100011000111001".

most significant stripe of code	1	1	1	1	1	1	1	1,	0	0	0	0	0	0	0	0,
-"- whith displacement	0	0	0	0,	1	1	1	1	1	1	1	1,	0	0	0	0
less significant stripe of code	1,	0	0,	1	1	1,	0	0	0,	1	1,	0	0	0,	1	1
-"- whit displacement	1	1,	0	0	0,	1	1,	0	0	0,	1	1	1,	0	0,	1
hexadecimal	B	9	8	A	E	F	D	C	4	6	7	5	1	0	2	3

1 - binary value "One"
0 - binary value "Zero"
, - change 1->0 or 0->1

In this way any four bit binary number is definitive related to sixteen positions at the code plate. It's a unit-distance code, changing only one bit from one entry to the next, as easily can be seen in the Karnaugh map:

|

_
  8
_____
  9
_____ |
|B
_|
  A
____

_

  C
____
  D
_____
  F
_____ |
|E
_|

_ |
|4
_|
  5
____
  7
_____
  6
_____

_

_
  0
_____ |
|1
_|
  3
____
  2
_____

_

|

To increase the resolution by two bits one further (fine, less significant) stripe of code is added and it's scanned by two further binary scanners. The bit stream on all further stripes of code ist like that at the second stripe of code "1", but four times finer and repeating.

The less significant stripe of code gives a on-bit-change for three consecutive steps. At every fourth step there is a change in one of the existing (coarse, more significant) stripes of codes.

	existing coarse
	digital steps   |       |       |       |       |       |
	bits at new      1,0 0,1 1 1,0 0 0,1 1,0 0 0,1 1 1,0 0, usw.
	code stripe      1 1,0 0 0,1 1,0 0 0,1 1 1,0 0,1 1 1,0
	new attached      , , ,   , , ,   , , ,   , , ,   , , ,
	fine digital steps

For further details read the german original text.

Reference:: "Abtastvorrichtung zur digitalen Weg- oder Winkelmessung"
DDR-Wirtschaftspatent
Anmeldetag: 29.04.1988 "H 03 M / 315 194 8"
Patentschrift DD 271 603 A1 vom 06.09.1989
A. Hok.

It took seven more years until a single track gray code (STGC) was described by Alain P. Hiltgen, Kenneth G. Paterson and M. Brandestini (1996).

"4" binary scanner for stripe 3	v				v
"3" most significant stripe
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	1	2	3	4
"1" stripe of code
"2" binary scanner for stripe 1	^				^

			\|
_	8 _____	9 _____	\| \|B _\|	A ____	_
	C ____	D _____	F _____	\| \|E _\|
_	\| \|4 _\|	5 ____	7 _____	6 _____	_
_	0 _____	\| \|1 _\|	3 ____	2 _____	_
			\|